U ovom članku iz našeg LoGeek Magazine - Broj #17, koristimo jednostavno logičko razmišljanje da objasnimo proces konstruisanja frakcionih indeksa. U ovom članku, istražićemo složenosti algoritma i njegove moguće primene, te ćemo se dotaći teme optimizacije veličine indeksa u graničnim slučajevima.
Pogledaćemo i kako se može modifikovati algoritam tako da podrži istovremeno korišćenje više korisnika. Na kraju ove studije, čitaoci će imati temeljno razumevanje principa po kojem funkcioniše frakciono indeksiranje.
Ako vas zanima svet tehnologije i želite da još dublje istražite slične sadržaje, pogledajte naš najnoviji broj LoGeek Magazine!
Predstavljanje problema
Izazov pred nama je sortiranje zapisa uz minimalno narušavanje postojećeg niza. Razmotrimo scenario gde je kolekcija redova poređana na osnovu polja indeksa, a cilj je premestiti ili umetnuti novi red bez uticaja na bilo koji drugi zapis.
Zašto nam je ovo potrebno?
Ovaj problem se javlja u raznim aplikacijama, posebno u kontekstu upravljanja ’’cloud’’ bazama podataka. U takvim okruženjima, gde promene redova povlače troškove, postaje očigledna važnost minimizovanja tih promena. Izvođenje potpunog renumerisanja redova nakon svake permutacije može dovesti do značajnog ekonomskog opterećenja, što stvara potrebu za efikasnijim pristupom.
Štaviše, izazov se proširuje na scenarije poput peer-to-peer sistema za uređivanje teksta. U ovim slučajevima, renumerisanje svih redova može dovesti do konflikta tokom sinhronizacije sa drugim peer-ovima, čime se nameće potreba za strategijom koja će umanjiti takve konflikte. Fokusiranjem samo na redove na kojima korisnik vrši akcije, cilj nam je da smanjimo učestalost konflikata i poboljšamo stabilnost sistema.
Postavlja se pitanje: da li je teoretski moguće postići takvo sortiranje uz minimalno ometanje?
Ideja izrade algoritma
Zaista, koncept frakcionalnog indeksiranja predstavlja jednostavno rešenje za naš problem sortiranja, slično načinu na koji bismo intuitivno pristupili zadatku na papiru. Na primer, zamislite da zapisujete listu stavki i shvatite da treba da ubacite dodatnu stavku između dve postojeće. Umesto da renumerišete celu sekvencu, jednostavno označite novu stavku novim frakcionalnim indeksom, kao što je 1.5.
Dok ova intuitivna metoda predstavlja osnovu frakcionalnog indeksiranja, njena direktna primena je otežana zbog ograničenja prikaza brojeva sa pokretnim zarezom. Brojevi sa pokretnim zarezom imaju ograničenu preciznost, što nam ne dozvoljava da ih beskonačno delimo a da se ne suočimo sa problemima kada je tačnost u pitanju.
Da bismo unapredili ovaj koncept, uvodimo pojam nedostižnih granica unutar opsega indeksa. Ovde označavamo nulu kao nedostižnu gornju granicu i jedan kao nedostižnu donju granicu, pod pretpostavkom da su redovi sortirani u rastućem redosledu indeksa.
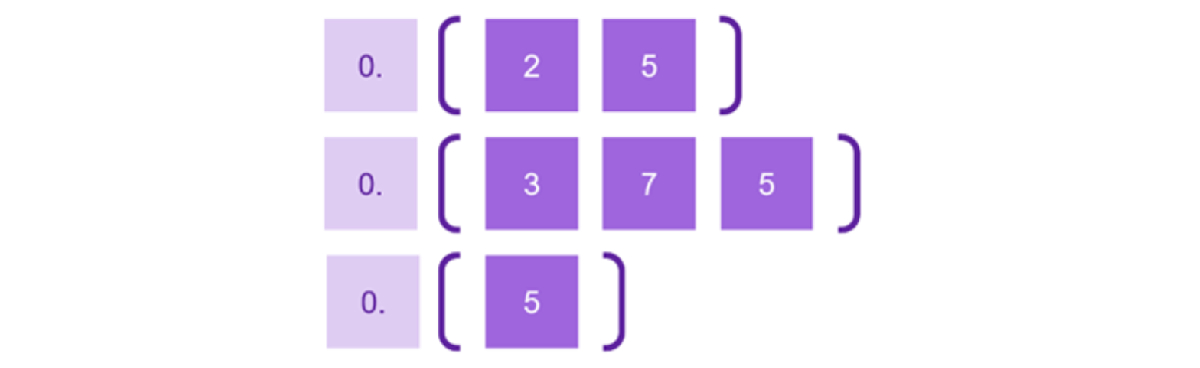
Razmotrimo scenario umetanja reda u praznu listu: Koristeći ove nedostižne granice, izračunavamo indeks kao srednju tačku između njih, što daje (0+1)/2=0.5. Slično tome, kada umećemo red iznad postojećeg, novi indeks se izračunava kao srednja tačka između nedostižne gornje granice i indeksa prethodnog reda, što daje rezultat (0+0.5)/2=0.25. Umetanje između postojećih redova uključuje izračunavanje proseka njihovih indeksa, što u ovom slučaju daje (0.25+0.5)/2=0.375.
Pažljivim ispitivanjem rezultujućih indeksa, primećujemo da je početni prefiks „nula-tačka” zajednički za sve indekse i može se zanemariti. Nadalje, predstavljanje završetaka indeksa kao string-ova ili byte nizova omogućava leksikografsko sortiranje, a pritom se očuva redosled indeksa. Ova fleksibilnost nam omogućava da proširimo numeričke indekse, uključujući karaktere iz skupova kao što je base64 ili čak proizvoljne bajtove, pod uslovom da naša aplikacija ili baza podataka podržava leksikografsko sortiranje takvih nizova.
Umetanje između indeksa
Kako izračunati novu vrednost indeksa između dva postojeća?
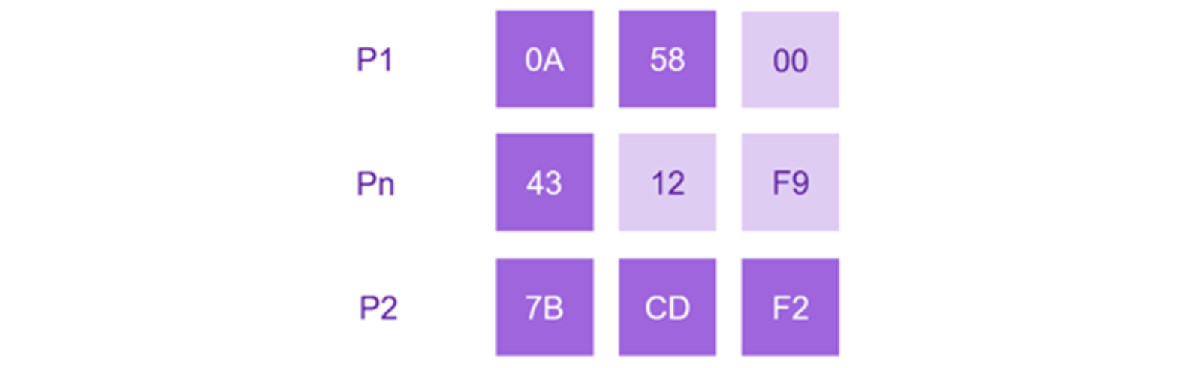
Da bismo odredili novu vrednost indeksa koja se nalazi između dva data indeksa, uzmimo kao primer bajt nizove P1=[0A 58] i P2=[7B CD F2]. Naš pristup koristi koncept racionalnih brojeva, gde prateće nule ne utiču na vrednost. Na primer, 0.1 i 0.100 su isti broj. Ovo nam omogućava da prilagodimo dužine indeksa dodavanjem nula po potrebi.
Usklađivanje dužina nizova je u suštini množenje naših racionalnih brojeva sa nekim zajedničkim osnovom kako bi postali celi brojevi. Tretirajući ove dužinski usklađene indekse kao velike cele brojeve, možemo odrediti njihovu aritmetičku sredinu:
Kao što je očigledno iz gore pomenute formule, postizanje ovoga zahteva samo izvođenje dve jednostavne operacije na nizovima bajtova: Sabiranje i pomeranje udesno za jedan bit. Obe operacije se lako mogu implementirati za proizvoljan set bajtova. Da biste to uradili, samo treba da izvršite operaciju na paru bajtova i prenesete ostatak na sledeći. Važno je napomenuti da nije neophodno zadržati sve dobijene brojeve. Kada se naiđe na bajt koji se razlikuje između P1 i P2, naredni bajtovi postaju nevažni i mogu se odbaciti.
Na primer, primena ove metode na našem primeru daje novi indeks:
Procena memorije
Najgori scenario algoritma nastaje kada se neprestano umeću novi redovi na istoj poziciji. Sa svakim umetanjem, opseg indeksa se sužava, što dovodi do produžavanja indeksa. Ali koliko brzo dolazi do ovog rasta?
Implementacijom algoritma sa bajt nizovima i izvođenjem 10.000 ubacivanja na početku liste, primećujemo da maksimalna veličina indeksa dostiže 1250 bajtova. Dakle, svako umetanje povećava dužinu indeksa za samo jedan bit.
Ovaj rezultat je pohvalan, jer jedan bit predstavlja minimalnu veličinu informacije i čini se da je teško postići bolji rezultat. Zapravo, skoro svi opisi algoritma se zaustavljaju ovde. Međutim, važno je posebno obraditi granične slučajeve, naročito umetanja na samom početku ili kraju liste. U ovim slučajevima, postoji jedna otvorena granica, što predstavlja priliku za optimizaciju.
Na primer, razmislite o peer-to-peer uređivaču teksta kao što je Notepad, ali gde su redovi sortirani prema frakcionalnom indeksu. Svaki put kada dodamo novi red, naš indeks se povećava za jedan bit. Ako ubacite red u sredinu, ništa se ne može uraditi povodom toga. Ali kada pišete tekst, dodavanje redova na samom kraju može biti verovatniji i prirodniji način. Stoga, optimizovanjem dodavanja novog indeksa na kraj liste, možemo smanjiti trošak memorije.
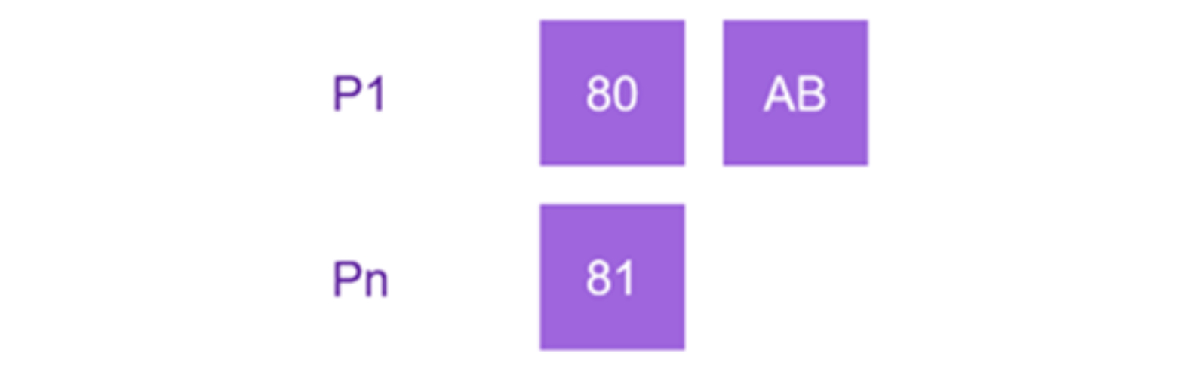
Razmotrimo jednostavan scenario gde je poslednji indeks u našoj listi označen kao P1=[80 AB], a mi želimo da generišemo sledeći indeks, Pn. Koristeći prethodni algoritam, dobijamo novu vrednost indeksa kao Pn=[C0]. Međutim, na prvi pogled, ovo povećanje izgleda preveliko. Umesto toga, potreban je suptilniji pristup: jednostavno povećavanje prvog bajta za jedan je dovoljno.
S obzirom na to da je početni indeks tačno u sredini opsega, ovo zapažanje omogućava približno 127 umetanja na kraju (ili početku) liste po prvom bajtu indeksa. Ovo je približno ekvivalentno povećanju od 0,06 bita po umetanju.
Osim toga, koristeći osobinu racionalnih brojeva, sledeći bajtovi su nule, što omogućava dodatnih 255 umetanja po bajtu indeksa. Shodno tome, ovo se prevodi u približno 0,03 bita po umetanju.
Suštinski aspekt ove modifikacije algoritma je povećanje indeksa za jedan bajt samo kada se dostignu granične vrednosti bajta (FF za umetanje na kraj ili 00 za umetanje na početak liste). Kao rezultat, retko dostizanje ekstremnih vrednosti smanjuje pojavu novih bajtova.
Korišćenjem parova bajtova za povećanje, efikasnost se značajno poboljšava. Ovaj pristup postiže izvanredne vrednosti od 0,0001 bita za svaki novi indeks. U takvim slučajevima, identifikovanje prvog bajta, isključujući granične vrednosti, dobija ključnu važnost, nakon čega se povećava sledeći bajt.
U suštini, granični slučajevi mogu biti efikasnije rešeni u poređenju sa osnovnim algoritmom. Međutim, ova optimizacija dolazi na račun početnih bajtova indeksa.
Za naš primer sa Notepad-om, to znači da će indeksi rasti samo za jedan bit pri umetanjima u sredinu teksta, ali dodavanje redova na kraj će koštati vrlo malo.
Drugi primer gde ovaj pristup može dobro funkcionisati je neka vrsta aplikacije za zadatke ili liste prioriteta. Zamislite listu sa tri zadatka koje stalno premeštate u nasumičnom redosledu. Bez optimizacije, svaki potez vas košta jedan bit u indeksu. Ali lista ima samo tri zadatka, pa je verovatnoća da pomerimo zadatak na sam početak ili kraj prilično velika. I ovaj optimizovani slučaj će skratiti indeks nazad na početnu veličinu bajtova.
Istovremeno uređivanje
Još jedan aspekt na koji se vredi osvrnuti jeste istovremeno uređivanje liste od strane više korisnika. Šta se dešava ako dva nezavisna klijenta pokušaju da umetnu red na isto mesto u isto vreme?
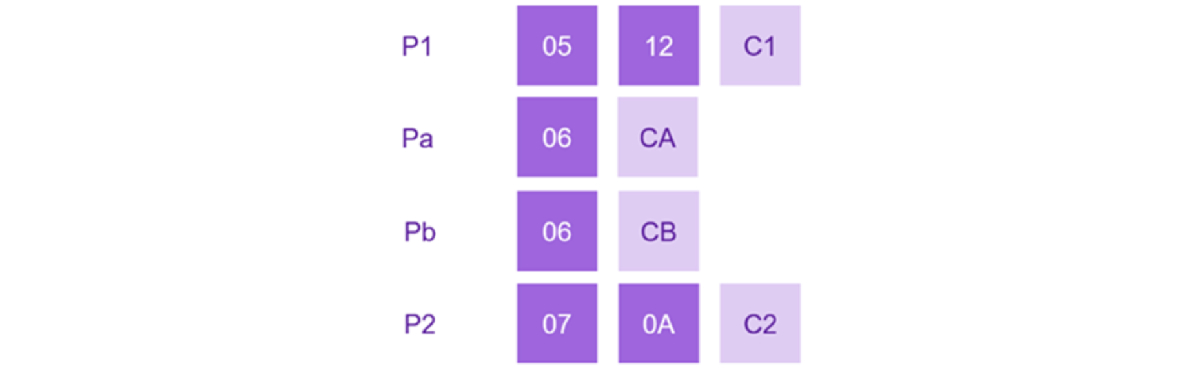
Ilustrujmo ovaj scenario jednostavnim primerom koji uključuje dve linije: P1=[05 12] i P2=[07 0A]. Pretpostavimo da dva klijenta pokušavaju da umetnu novu liniju između P1 i P2.
Prema našem algoritmu, s obzirom na iste ulazne podatke, oba klijenta će dobiti iste vrednosti za umetnute indekse: Pa=Pb=[06]. Ovo postavlja dva značajna problema. Prvo, vodi do nedefinisanog redosleda redova jer su indeksi identični, što otežava određivanje koji bi trebalo da bude viši. Drugo, još važnije, identični indeksi onemogućavaju umetanje bilo čega između njih.
Da bismo rešili ovaj izazov, neophodno je osigurati da generisani indeksi budu jedinstveni. Ovde koristimo ključnu karakteristiku naših indeksa: ako imamo listu jedinstvenih vrednosti, dodavanje bilo kojeg sufiksa bilo kojem indeksu neće promeniti redosled redova. Stoga možemo uvesti male, jedinstvene varijacije za svakog klijenta, i tako osigurati da generisane vrednosti budu jedinstvene.
Takvi jedinstveni sufiksi mogu se generisati svaki put kada se kreira zapis ili jednom prilikom pokretanja aplikacije. Dužina ovih sufiksa može varirati, što balansira verovatnoću slučajnog konflikta sa dodatnom memorijom koja je potrebna.
Na primer, u jednom od mojih projekata, implementirao sam generisanje jedinstvenog sufiksa dužine 6 bajtova, prema sledećim pravilima:
Prva dva bita su konstantna nula-jedan. Ovo je potrebno za rešavanje degenerisanih slučajeva kada sufiks sadrži sve nule ili sve jedinice, pošto znamo da takvi sufiksi mogu značajno uticati na dužinu indeksa na početku ili kraju liste.
Narednih 21 bitova je nasumično generisano. Ovaj redosled nam omogućava da smanjimo očekivanu dužinu indeksa tako da postoji manja verovatnoća za identične bajtove, i možemo skratiti indeks ranije kada umetnemo red između dva postojeća.
I poslednjih 25 bitova predstavlja vreme u Unix formatu. Ovo je godišnji ciklus, ali nam omogućava da značajno smanjimo verovatnoću generisanja duplikata sufiksa, jer se računanje vrši jednom, prilikom pokretanja aplikacije.
Zaključak
Na kraju smo uspešno razvili algoritam koji efikasno sortira zapise sa minimalnim izmenama liste. Osvrtom na izazove kao što su istovremene operacije klijenata, poboljšali smo fleksibilnost i efikasnost algoritma. Osim toga, optimizovali smo slučajeve umetanja na početak ili kraj liste, što osigurava jače performanse u različitim scenarijima.
Zanima vas svet tehnologije i želite da dublje istražite sličan sadržaj? Pročitajte ceo broj našeg LoGeek Magazina - Broj #17 i pratite nas na LinkedIn-u.
Reference
https://www.figma.com/blog/realtime-editing-of-ordered-sequences/



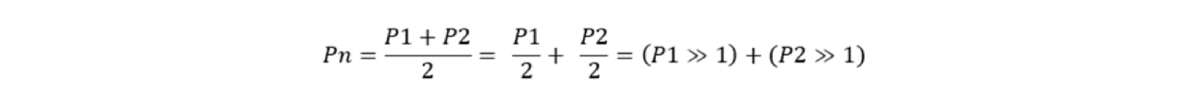






0 komentara